CLD | Manish Nagaraj

At a glance — why CLD matters
Training on everything is costly and often unnecessary. CLD (Correlation of Loss Differences) finds a small subset of training data that behaves like the full dataset by watching how losses change over time. If a sample’s loss rises/falls in sync with how validation loss moves, it’s likely carrying useful signal. Keep those, skip the rest.

What you get: core sets that typically match or beat strong baselines across subset sizes, transfer to new architectures, and can be computed with lightweight logs instead of gradients/Hessians.
What it saves: selection compute, storage, and later training time.

Motivation

Large models are constrained by compute, memory, and wall time. The pragmatic question isn’t just “how do I train?” but “what do I really need to train on?” Many selection methods rely on gradients, second-order information, or pairwise features—powerful but heavy.
CLD keeps it simple: it needs only per-sample losses over checkpoints (scalars you likely log already).

CLD at a glance: high vs. low CLD samples and coreset effect

Schematic intuition: “high-CLD” samples move in step with validation dynamics; “low-CLD” do not.

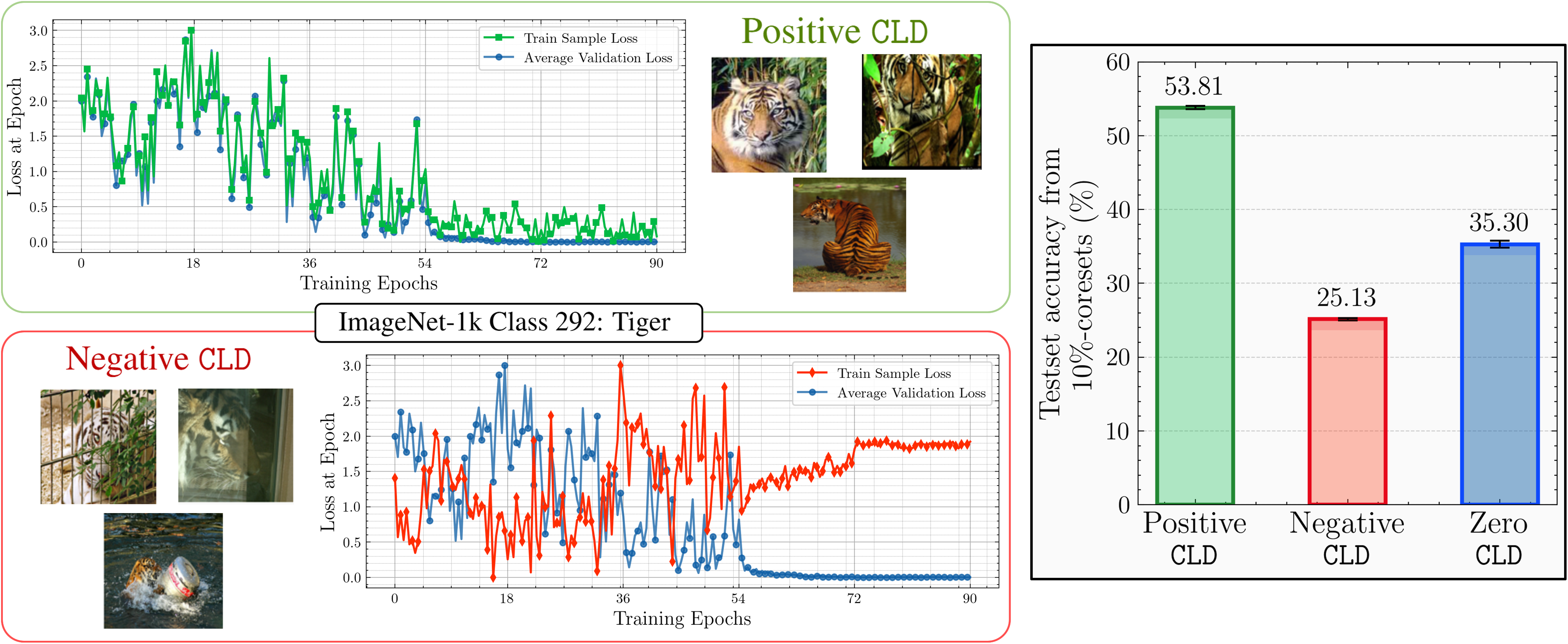
What CLD actually does

Think of training as a timeline. At each checkpoint, every sample’s loss goes up or down a little. Validation loss also moves.
If a sample’s loss-change pattern over time correlates with the validation loss-change pattern for its class, that sample is influential for generalization. CLD keeps the most aligned ones.

Minimal math (for completeness). For each training sample $z_m$, $\Delta(z_m) = \big[\ell(\theta_1, z_m) - \ell(\theta_0, z_m), \ldots, \ell(\theta_T, z_m) - \ell(\theta_{T-1}, z_m)\big].$ Let $\Delta’_{V,c}$ be the class-wise validation loss differences. The CLD score is the Pearson correlation $\mathtt{CLD}(z_m) = \rho\!\big(\Delta(z_m),\, \Delta'_{V,c}\big).$ We keep the top-$k_c$ per class and union them into the coreset $C$.

Why this is nice for systems: it uses only loss scalars you can log with negligible overhead; no per-sample gradients or Hessians.

How CLD is implemented

Train a proxy/backbone (e.g., ResNet-18) and log per-sample train loss each epoch (or every few epochs).
Create a small per-class validation set and log its per-sample validation loss similarly.
Compute loss differences (checkpoint-to-checkpoint), correlate train vs. validation within each class, and keep top-$k_c$.
Train your target model on the union of these per-class picks.

Tip: You can compute CLD from early checkpoints (e.g., first 30–45 of 90) or subsample the timeline (e.g., every 2–3 epochs) with little impact on quality.

Why CLD preserves optimization

Under standard smoothness/bounded-gradient assumptions, if you train on high-CLD subsets, you follow the same optimization path as the full dataset up to a small, explicit deviation. Two drivers control that deviation:

Alignment ($\kappa$): how strongly your chosen samples’ loss changes line up with validation. Better alignment → smaller gap.
Validation representativeness ($\delta$): whether the validation signal actually reflects what you care about.

Takeaway: high CLD is a principled way to track full-data training with far fewer samples.

Results & Observations

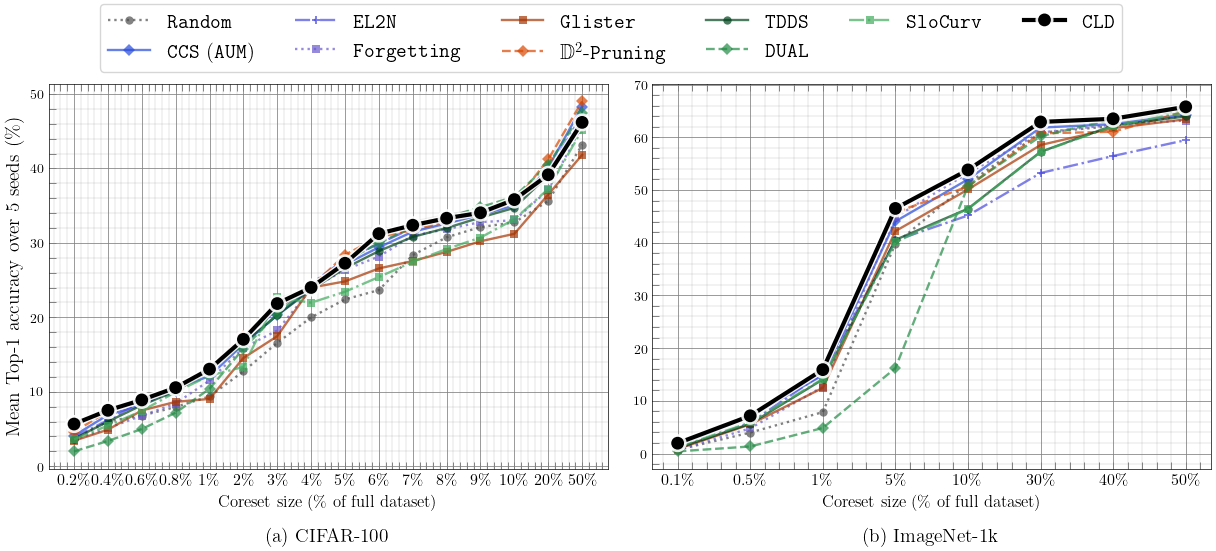
Benchmarks & setup. CIFAR-100 and ImageNet-1k; per-class validation splits (10% and 1% respectively); 5 seeds; ResNet-18 for scoring/training unless noted; subset sizes from 0.2–100% (CIFAR-100) and 0.1–100% (ImageNet-1k).

Accuracy vs SOTA: CLD typically matches or outperforms score-based, optimization-based, and training-property baselines across subset sizes; when not leading, it’s usually within ~1% of the best.
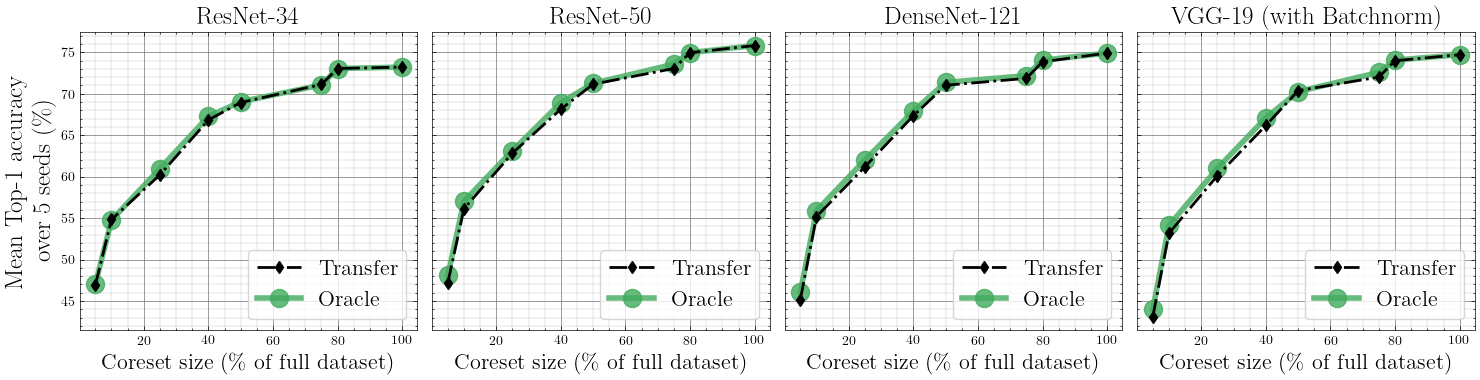
Transferability: Coresets selected with ResNet-18 transfer to ResNet-34/50, VGG-19, DenseNet-121 with <~1% gap to that model’s own (“oracle”) selection.
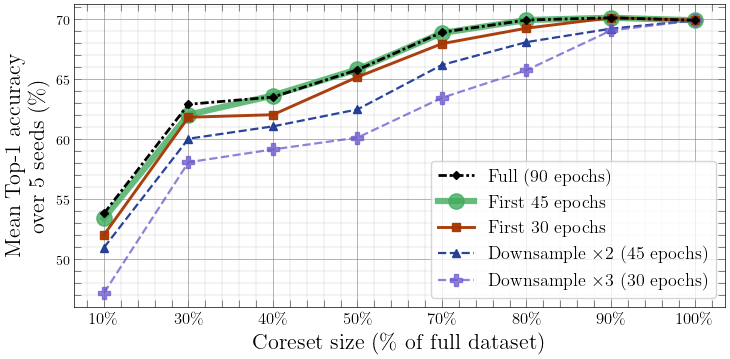
Stability & early checkpoints: Using only the first 30–45 of 90 epochs or 2–3× checkpoint subsampling yields nearly identical results.
Bias & class balance: Per-class validation alignment acts as a bias reducer; adding external stratified sampling often hurts CLD.

CLD vs baselines: CIFAR-100 & ImageNet-1k

Cross-architecture transfer: ResNet-18 → {ResNet-34/50, VGG-19, DenseNet-121}

CLD is competitive across subset sizes and transfers across architectures within ~1%.

Compute & storage efficiency

CLD logs one scalar per sample per checkpoint (plus validation scalars). No gradients, Hessians, or feature banks. Selection compute is proxy-only; once you have the subset, train your target model as usual. In end-to-end compute vs. accuracy, CLD sits near the Pareto frontier; early-epoch CLD (e.g., 45/90) keeps accuracy with ~half the selection compute.

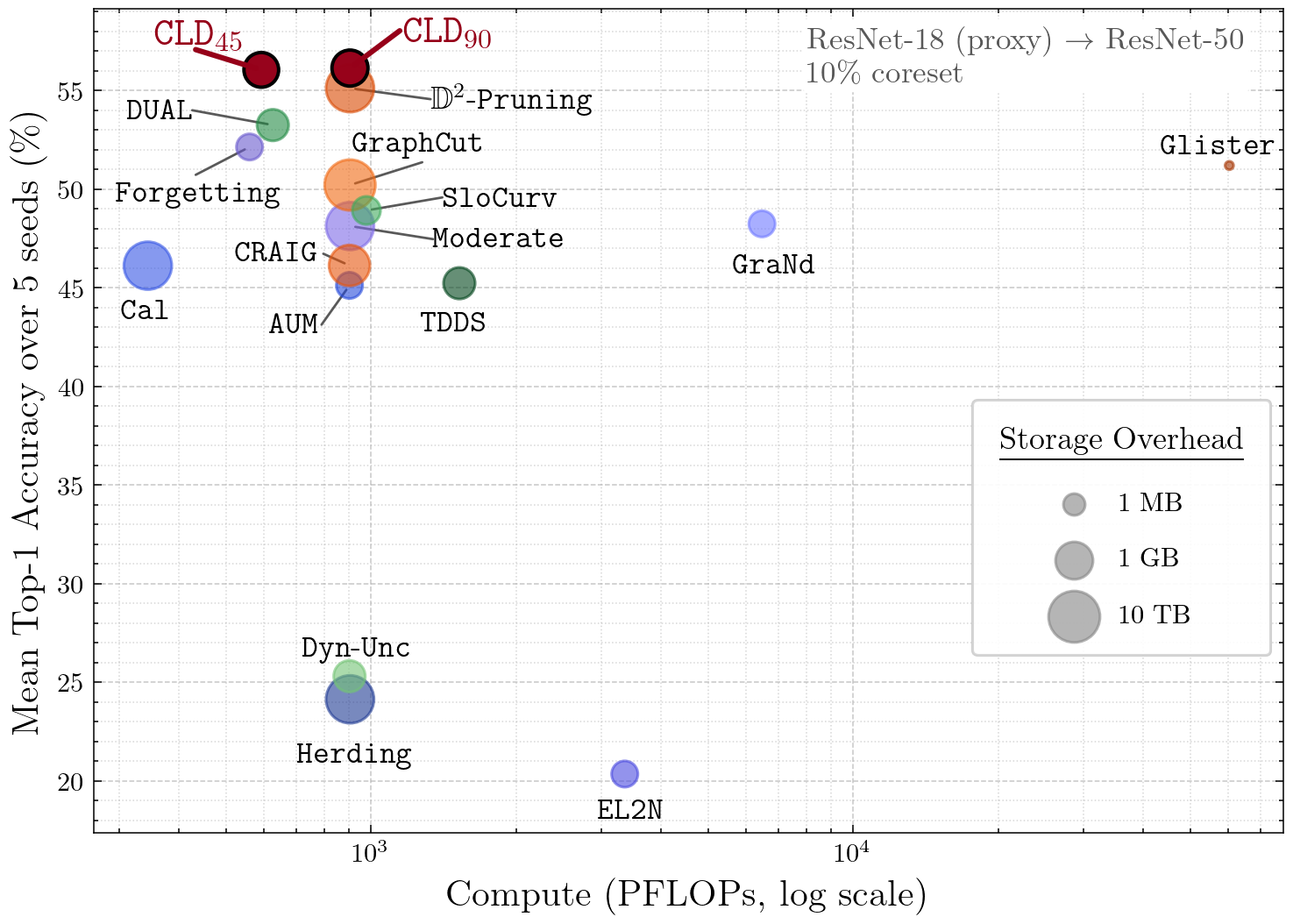
Accuracy vs end-to-end compute; bubble size=selection-stage storage

Practical guidance

Proxy model. A light backbone (ResNet-18) is enough to score; the coreset transfers well to bigger targets.
Validation set. Keep it representative per class. Heavy skew toward atypical/mislabeled samples hurts CLD. Proportional sampling to the pool usually works best.
Timeline budget. Short on time? Use early checkpoints or subsample; CLD is robust.
No extra stratification. Percentile-style stratification layered on top of CLD often reduces accuracy.

Stability with early/subsampled checkpoints

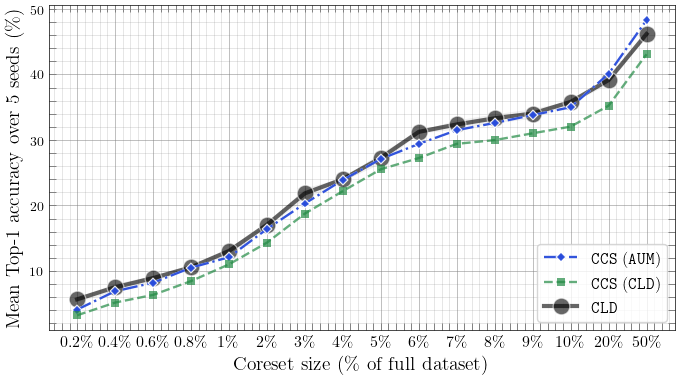
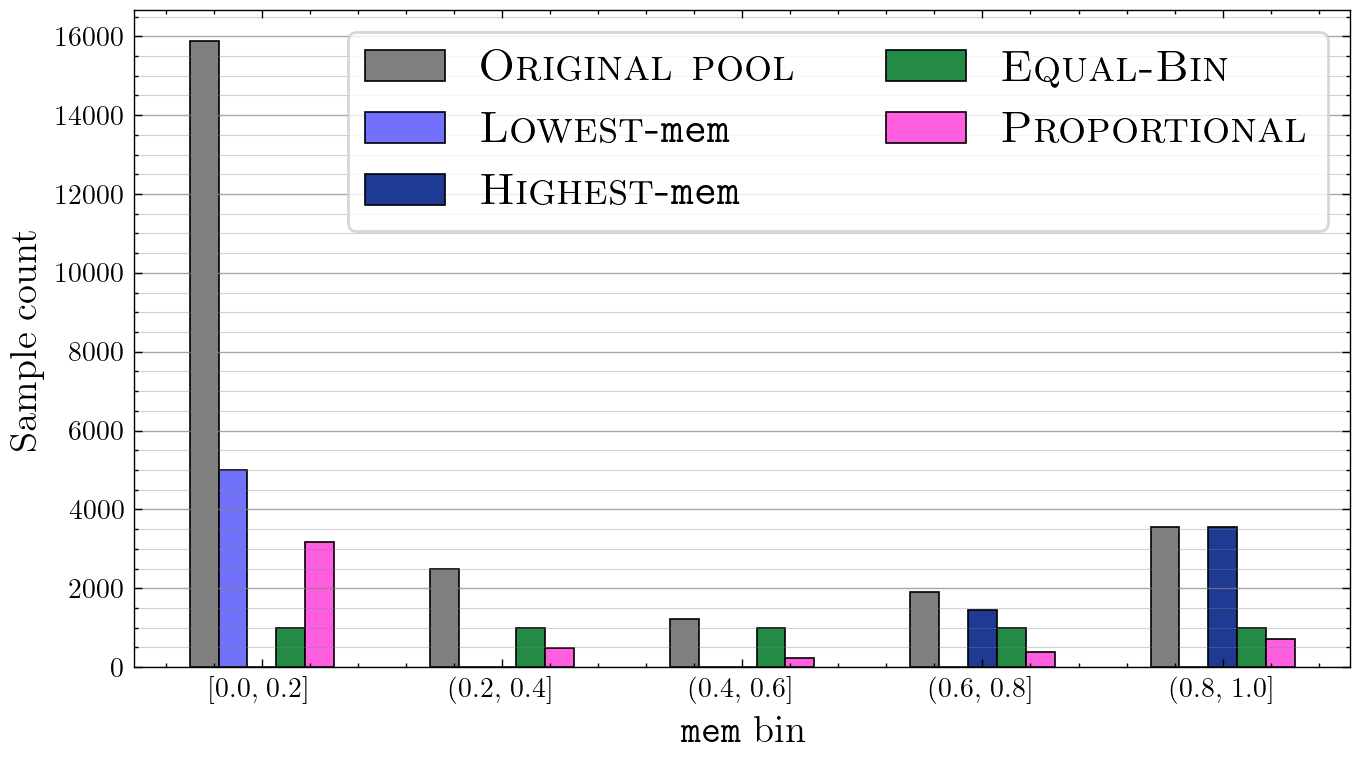
Why proxy quality matters

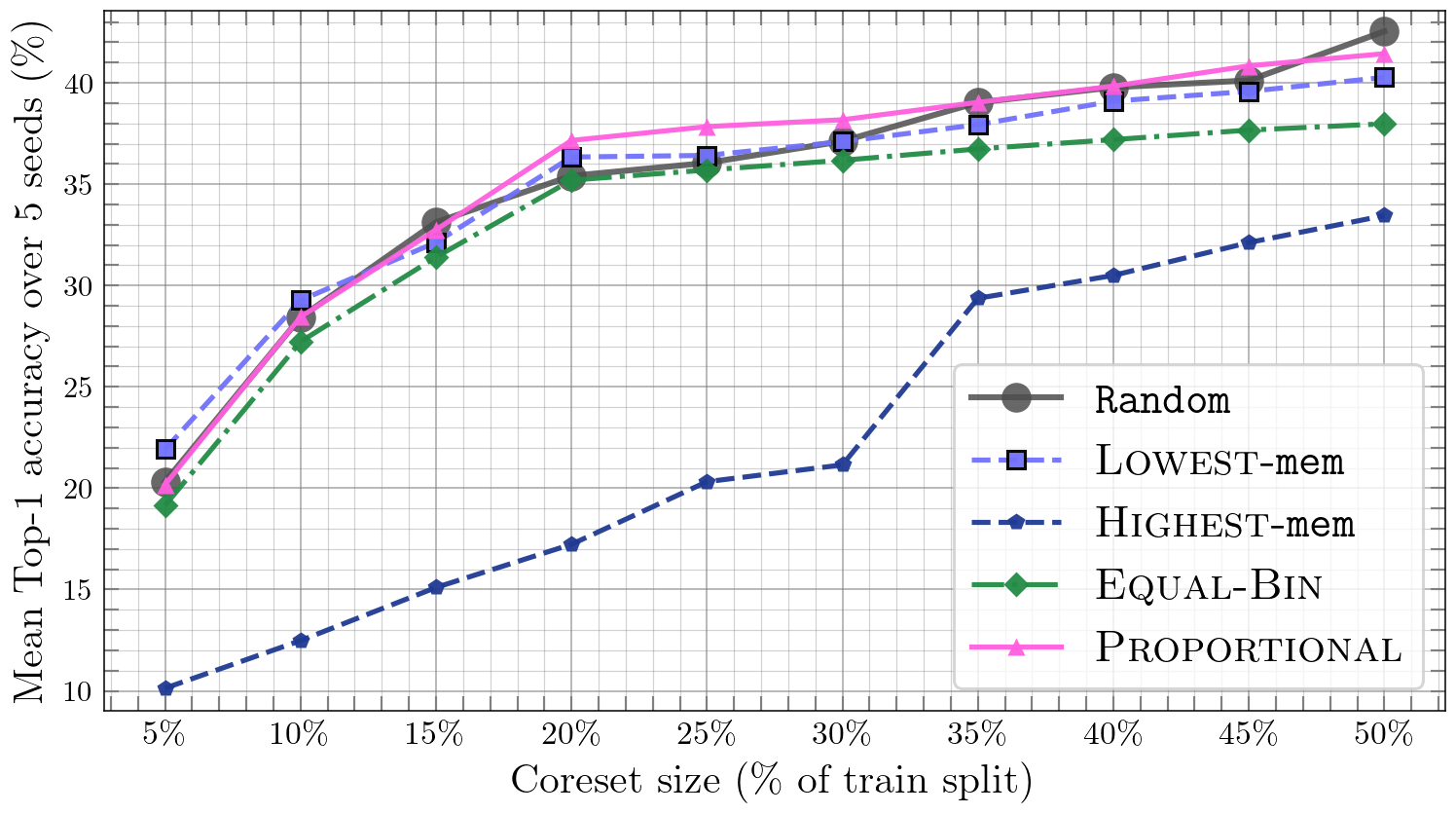
Changing the validation composition using memorization-based heuristics shifts downstream CLD performance. Proportional sampling to the pool is most reliable; highest-memorization-only tends to hurt, while a light mix can help long-tail behavior. The message: validation representativeness directly impacts CLD.

Effect of validation composition on CLD coresets

You can find more details in the full paper: (Nagaraj et al., 2025)

Deep learning models achieve state-of-the-art performance across domains but face scalability challenges in real-time or resource-constrained scenarios. To address this, we proposeCorrelation of Loss Differences (CLD), a simple and scalable metric for coreset selection that identifies the most impactful training samples by measuring their alignment with the loss trajectories of a held-out validation set. CLD is highly efficient, requiring only persample loss values computed at training checkpoints, and avoiding the costly gradient and curvature computations used in many existing subset selection methods. We develop a general theoretical framework that establishes convergence guarantees for CLD-based coresets, demonstrating that the convergence error is upper-bounded by the alignment of the selected samples and the representativeness of the validation set. On CIFAR-100 and ImageNet-1k,CLD-based coresets typically outperform or closely match state-of-the-art methods across subset sizes, and remain within 1% of more computationally expensive baselines even when not leading. CLD transfers effectively across architectures (ResNet, VGG, DenseNet), enabling proxy-to-target selection with < 1% degradation. Moreover, CLD is stable when using only early checkpoints, incurring negligible accuracy loss. Finally, CLD exhibits inherent bias reduction via per-class validation alignment, obviating the need for additional stratified sampling. Together, these properties make CLD a principled, efficient, stable, and transferable tool for scalable dataset optimization.