TRIM | Manish Nagaraj

At a glance — why TRIM matters
Instruction tuning works best with small, high-quality data, not just more data. TRIM (Token Relevance via Interpretable Multi-layer attention) builds a coreset by matching token-level patterns from a tiny target set (5–10 samples) against a large candidate pool — using only forward passes. Result: coresets that can beat gradient/Hessian baselines and, in some settings, even surpass full-data fine-tuning at a fraction of the cost.

Motivation

Most selection methods rank whole examples using coarse, sample-level signals (gradients, Hessians, per-sample losses). That’s pricey and misses the fact that a few tokens often carry the signal (reasoning steps, operators, entities). TRIM flips the perspective: it scores tokens first—then rolls them up into example relevance. You keep examples that contain task-defining tokens; you skip those that don’t.

TRIM overview: attention-derived token saliency → token-class fingerprints → token-to-fingerprint matching → example score

TRIM in two stages: (a) attention-derived token saliency, (b) token-class fingerprints from a few target samples, (c) cosine match for each token in a candidate, (d) mean–max pooling to score the example.

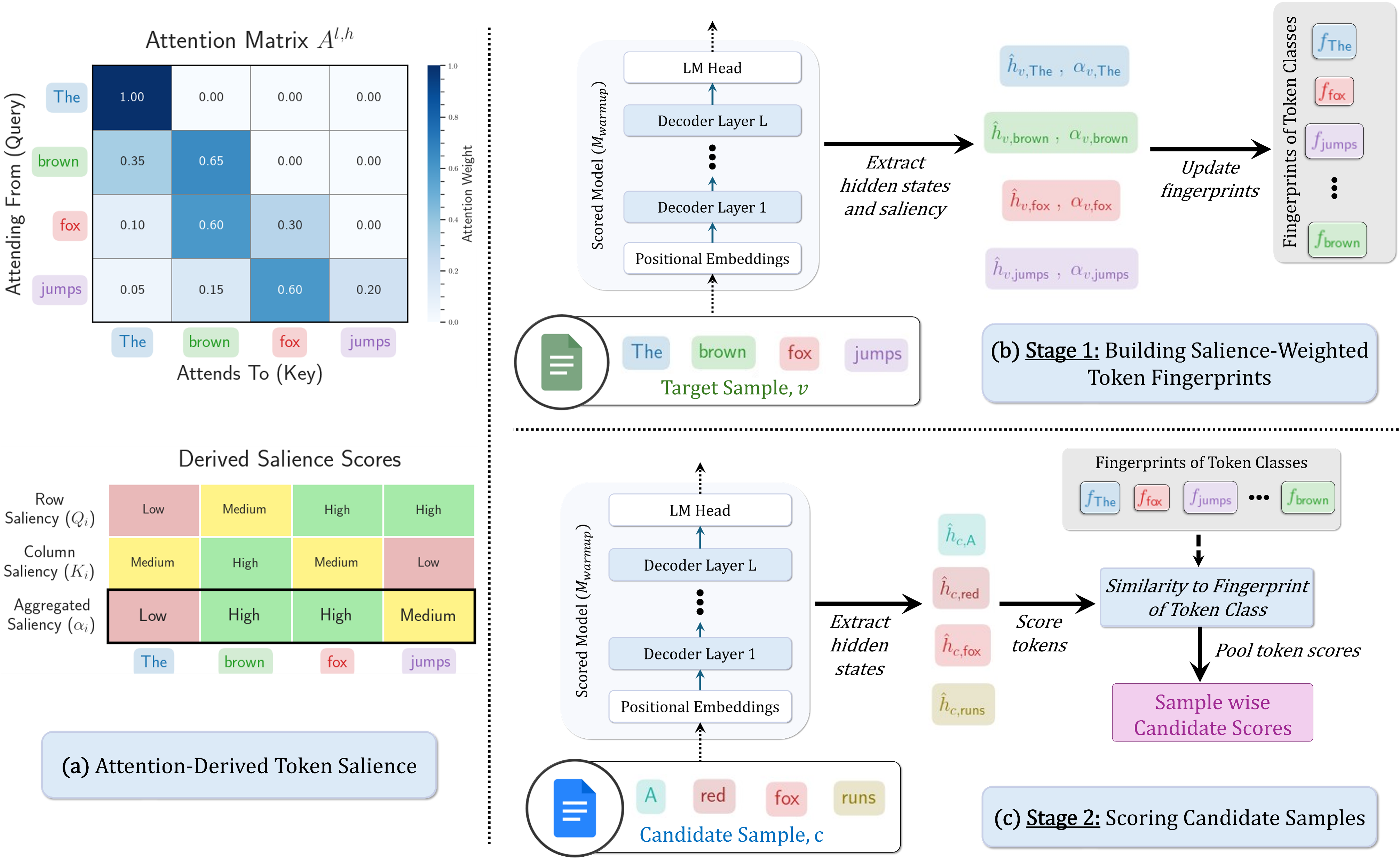
What TRIM actually does

From the last $L$ layers of a warmed-up model, read attention to compute token saliency that blends two views:
- Row saliency (how sharply a token allocates attention).
- Column saliency (how much attention a token receives).
With 5–10 target samples, build one fingerprint per token class: a saliency-weighted mean of last-layer token states that captures the task’s structural patterns (e.g., operators, reasoning markers).
For each candidate example, compare each token’s hidden state to its token-class fingerprint (cosine). Pool token scores (mean + max) → example score → rank → coreset.

Let $\alpha_i = \tfrac{1}{2}Q_i + \tfrac{1}{2}K_i$ be the aggregated saliency for token $i$ (row $Q$ + column $K$).
For token class $t$ with target tokens $(v,i)\in O_t$ and last-layer states $h_{v,i}$, the fingerprint is $f_t \;=\; \frac{\sum_{(v,i)\in O_t} \alpha_{v,i}\,\hat h_{v,i}}{\left\lVert \sum_{(v,i)\in O_t} \alpha_{v,i}\,\hat h_{v,i} \right\rVert_2}, \quad \text{where } \hat h_{v,i} = \frac{h_{v,i}}{\|h_{v,i}\|_2}.$ For candidate token $j$ with class $t_j$, score $s_j=\cos(\hat h_{c,j}, f_{t_j})$ (or use a nearest fingerprint with penalty $\lambda$ if $t_j$ unseen). Example score: $S(c) \;=\; \tfrac12\,\mathrm{mean}(\{s_j\}) \;+\; \tfrac12\,\max(\{s_j\}).$ (One forward pass per candidate; no gradients.)

Results & observations

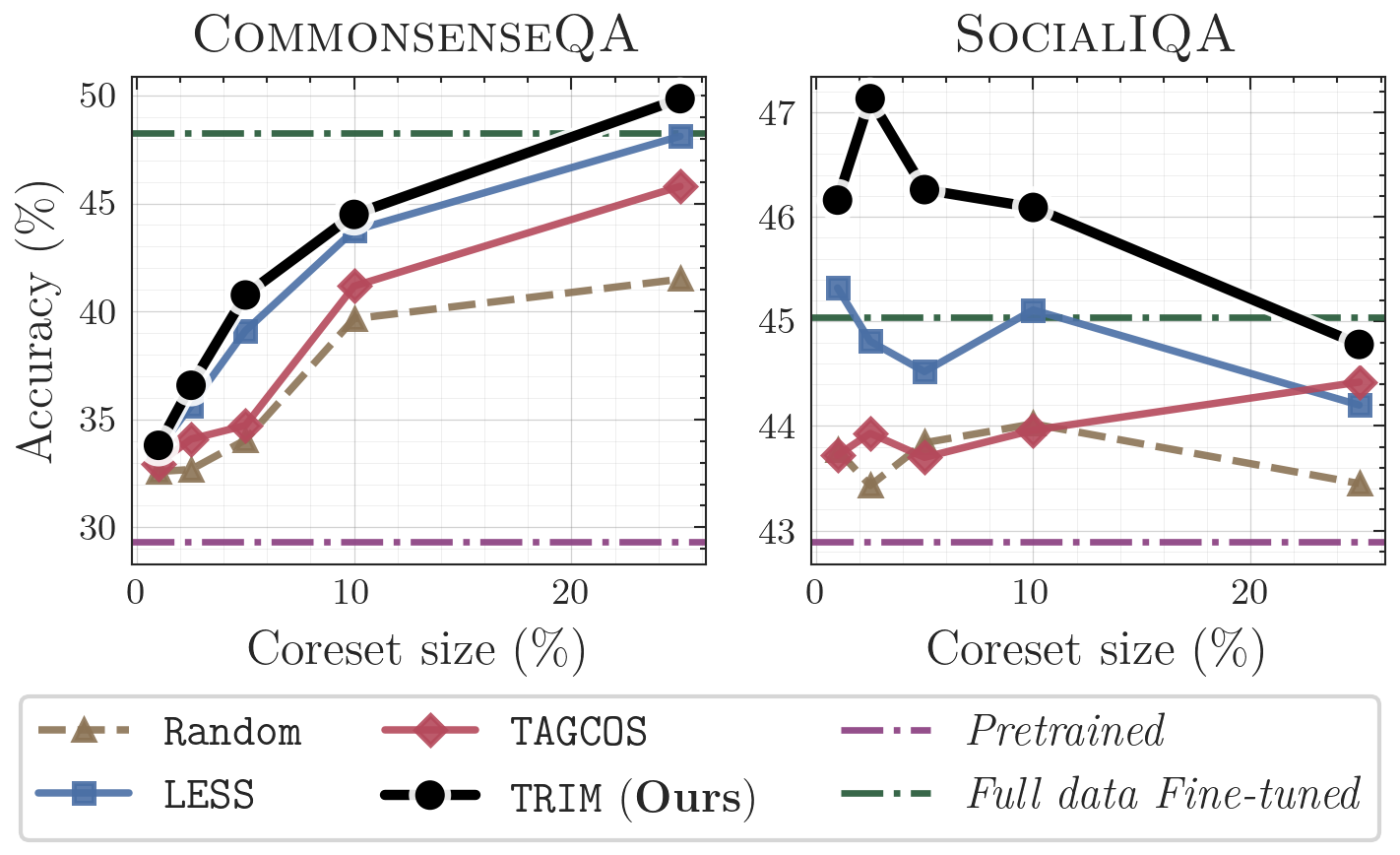
Budgeted accuracy (5%) — On LLAMA-3.2-1B, TRIM attains the best macro-average and is the only method whose 5% coresets surpass full-data on two tasks (SocialIQa and HellaSwag). Across budgets, TRIM consistently outperforms top baselines.
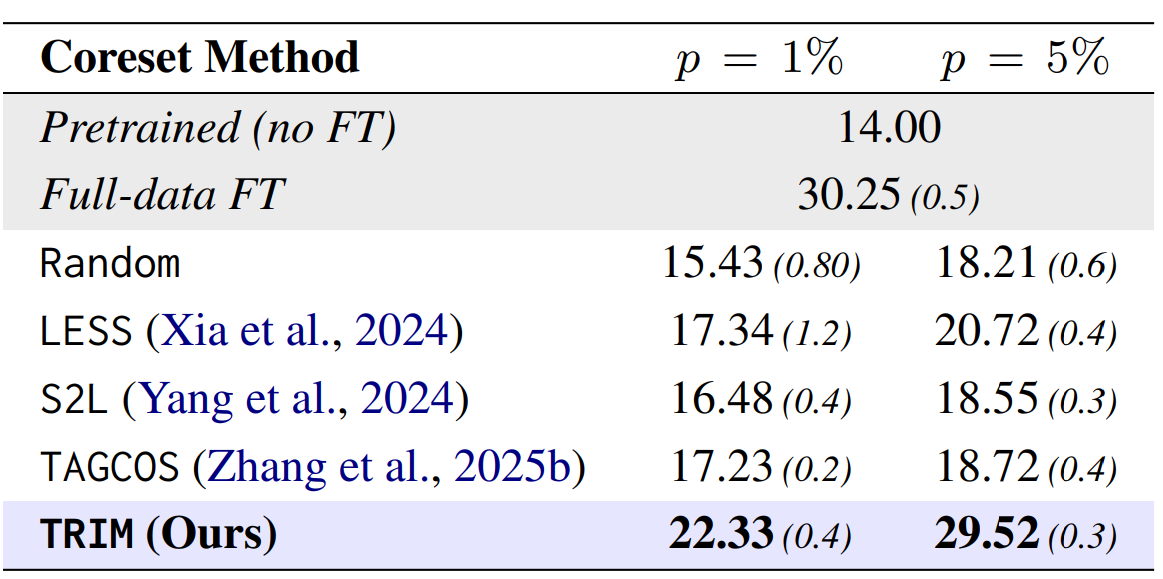
Low-overlap transfer (GSM8K) — From a non-math corpus, 5% TRIM nearly matches full-data; at 1% and 5% it beats gradient/trajectory baselines by large margins.
Cross-model transfer — A single 5% coreset chosen by a 1B scorer transfers to LLAMA-3.1-8B and Mistral-7B, matching or beating the in-model oracle.
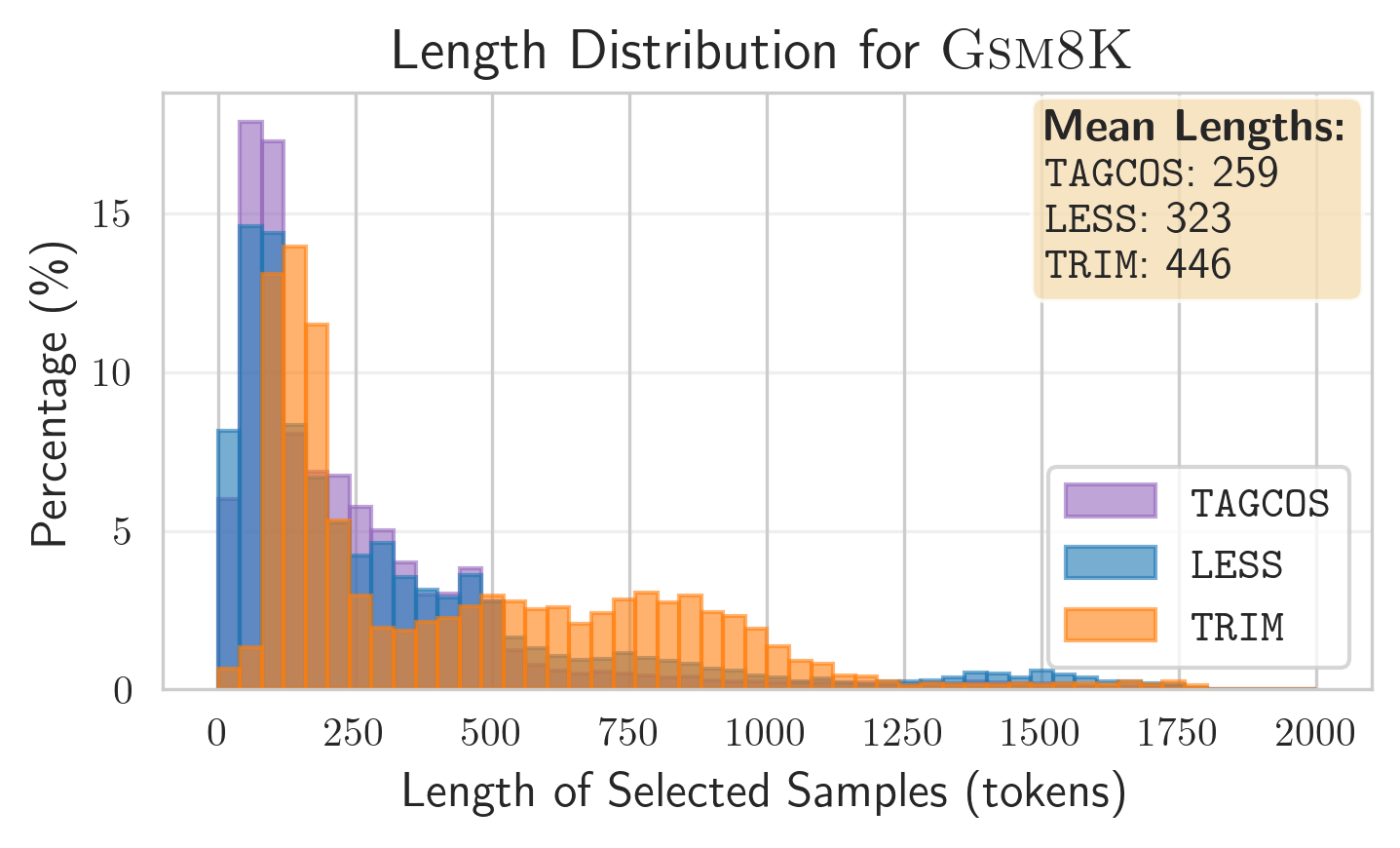
Length bias — TRIM’s token-centric scoring is length-agnostic; selected examples are longer and richer than gradient baselines, avoiding the short-sequence bias.

TRIM vs. baselines across coreset budgets (CSQA & SocialIQa)

Low-overlap out-of-domain (GSM8K) — TRIM from non-math pool

Cross-model/scale transfer — 1B scorer → larger targets

Length distribution of selected coresets — TRIM vs gradient baselines

Efficiency (why this scales)

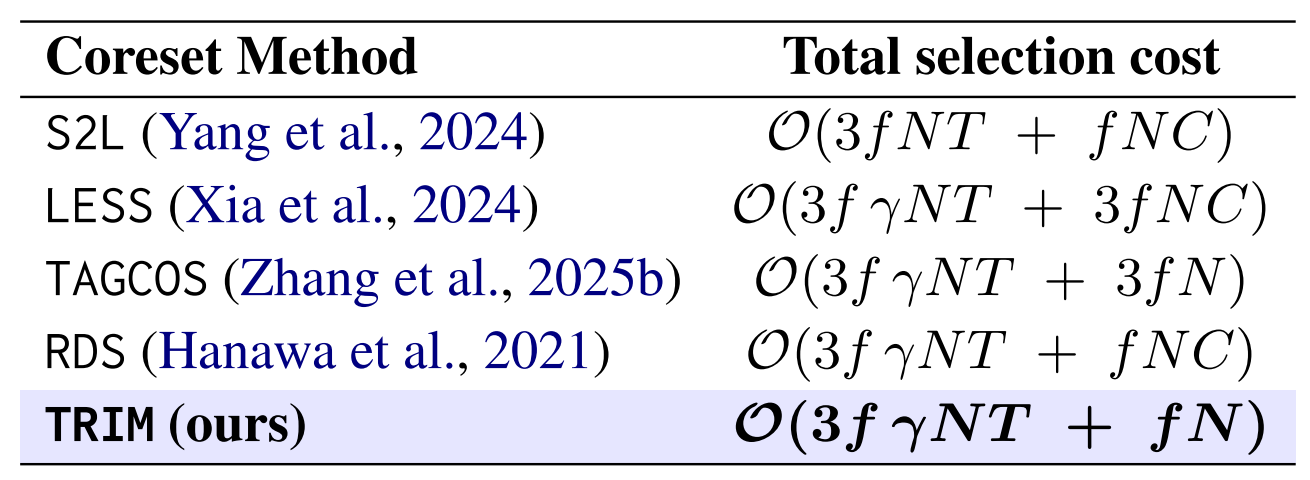
TRIM is forward-only at scoring time (one pass per candidate, single checkpoint), so the selection stage scales as $\mathcal{O}(fN)$ after a brief warmup. Gradient baselines (e.g., LESS/TAGCOS) require backward passes and/or multiple checkpoints $C$, pushing cost toward $\mathcal{O}(3fNC)$; trajectory methods (e.g., S2L) can require training on all candidates for logs. In practice, TRIM is orders of magnitude faster on large pools.

Asymptotic selection cost comparison (scoring model forward cost=f)

Practical guidance

Target set size. 5–10 target samples per task suffice to build robust fingerprints; make them representative of the reasoning style you care about.
Scope control. You can score prompt-only, response-only, or all tokens. For math/reasoning (GSM8K), response-focused often helps.
Unseen tokens. Use the nearest fingerprint in embedding space with a penalty $\lambda\in(0,1]$.
Pooling. Mean + max is a good default; if your data has rare “tell-tale” tokens, you can upweight the max term.
Warmup. A brief 5% warmup stabilizes attention and hidden states for scoring; full re-training is not needed.

You can find more details in the full paper: (Nagaraj et al., 2025)

Instruction tuning is essential for aligning large language models (LLMs) to downstream tasks and commonly relies on large, diverse corpora. However, small, high-quality subsets, known as coresets, can deliver comparable or superior results, though curating them remains challenging. Existing methods often rely on coarse, sample-level signals like gradients, an approach that is computationally expensive and overlooks fine-grained features. To address this, we introduce TRIM (Token Relevance via Interpretable Multi-layer Attention), a forward-only, token-centric framework. Instead of using gradients, TRIM operates by matching underlying representational patterns identified via attention-based "fingerprints" from a handful of target samples. Such an approach makes TRIM highly efficient and uniquely sensitive to the structural features that define a task. Coresets selected by our method consistently outperform state-of-the-art baselines by up to 9% on downstream tasks and even surpass the performance of full-data fine-tuning in some settings. By avoiding expensive backward passes, TRIM achieves this at a fraction of the computational cost. These findings establish TRIM as a scalable and efficient alternative for building high-quality instruction-tuning datasets.

Motivation

What TRIM actually does

Results & observations

Efficiency (why this scales)

Practical guidance

References

2025